Abstract
It was found that Maxwell's equation do not provide satisfactory description of Electro-Magnetic waves in the vacuum (EM waves).
Introduction
The common view of modern science is that Maxwell's equations provide a complete description of electromagnetic phenomena. This article is however not arguing with such broad statement, but just consider applicability of Maxwell's equations to the electromagnetic waves in vacuum.
Some History
It is very interesting how the equations were derived. The derivation appeared in the Maxwell's paper “On Faraday's Lines of Force.”
We should thus obtain a geometrical model of the physical phenomena, which would tell us the direction of the force, but we should still require some method of indicating the intensity of the force at any point. If we consider these curves not as mere lines, but as fine tubes of variable section carrying an incompressible fluid, then, since the velocity of the fluid is inversely as the section of the tube, we may make the velocity vary according to any given law, by regulating the section of the tube, and in this way we might represent the intensity of the force as well as its direction by the motion of the fluid in these tubes.
The result of such modeling was considered by Maxwell as mathematical tools for experimental physics.
If the results of mere speculation which I have collected are found to be of any use to experimental philosophers, in arranging and interpreting their results, they will have served their purpose, and a mature theory, in which physical facts will be physically explained, will be formed by those who by interrogating Nature herself can obtain the only true solution of the questions which the mathematical theory suggests.
The fluid used for the modeling of electromagnetic phenomena could have any properties we want it to have.
The properties of the fluid are at our disposal, we have made it incompressible, and now we suppose it produced from nothing at certain points and reduced to nothing at others.
Later in the “A Dynamical Theory of the Electromagnetic Field” Maxwell said:
The theory I propose may therefore be called a theory of the Electromagnetic Field, because it has to do with the space in the neighbourhood of the electric or magnetic bodies, and it may be called a Dynamical Theory, because it assumes that in that space there is matter in motion, by which the observed electromagnetic phenomena are produced.
Poetry
Although it is not related to the article, just could not skip the poetry of James Clerk Maxwell.
THE SONG OF THE ATLANTIC TELEGRAPH COMPANY
(u) = “Under the sea,”
I.
2(u)
Mark how the telegraph motions to me,
2(u)
Signals are coming along,
With a wag, wag, wag;
The telegraph needle is vibrating free,
And every vibration is telling to me
How they drag, drag, drag,
The telegraph cable along,
II.
2(u)
No little signals are coming to me
2(u)
Something has surely gone wrong,
And it’s broke, broke, broke;
What is the cause of it does not transpire,
But something has broken the telegraph wire
With a stroke, stroke, stroke,
Or else they’ve been pulling too strong.
III.
2(u)
Fishes are whispering. What can it be,
2(u)
So many hundred miles long?
For it’s strange, strange, strange,
How they could spin out such durable stuff,
Lying all wiry, elastic, and tough,
Without change, change, change,
In the salt water so strong.
IV.
2(u)
There let us leave it for fishes to see;
2(u)
They’ll see lots of cables ere long,
For we’ll twine, twine, twine,
And spin a new cable, and try it again,
And settle our bargains of cotton and grain,
With a line, line, line,
A line that will never go wrong.
Equations
Maxwell's equations in free space (zero currents and zero charges) could be written as follow:
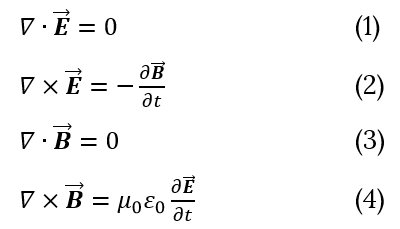
Mathematical operators used in the above notation are defined in the following way:
A vector field V(x,y,z,t) associates a vector
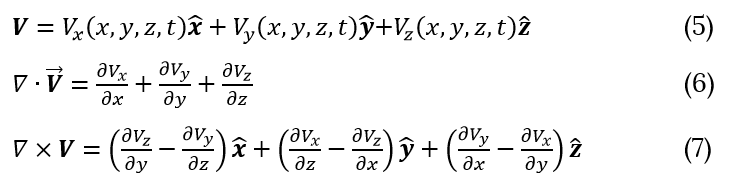
The theory telling us that EM waves are solutions of Maxwell's equations, which are the fundamental equations of electrodynamics. EM waves require no medium, they can travel through empty space. Sinusoidal plane waves are one type of electromagnetic waves. Not all EM waves are sinusoidal plane waves, but all electromagnetic waves can be viewed as a linear superposition of sinusoidal plane waves traveling in arbitrary directions. A plane EM wave traveling in the x-direction is of the form
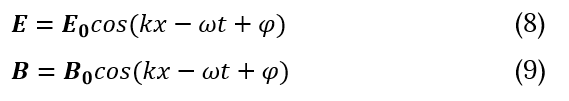
where

Sine?
Why science textbooks always mentioned sine function as the solution for Maxwell's equations? I don't have the answer for that, probably because experiments show sine character of EM waves. And why do we need superposition of plane waves?
Below I am going to demonstrate that almost any function satisfied to the Maxwell's equation.
Orthogonal Functions
I will start with classic solution similar to plane wave (8-9) where wave propagates along x-axis, electric field directed along y-axis and magnetic field directed along z-axis (10-11).
The difference I am going to investigate is not-sine dependency on x-coordinate and time.
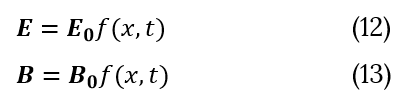
With vectors E0 and B0 perpendicular to each other and defined as before (10-11) the Maxwell's equations become:
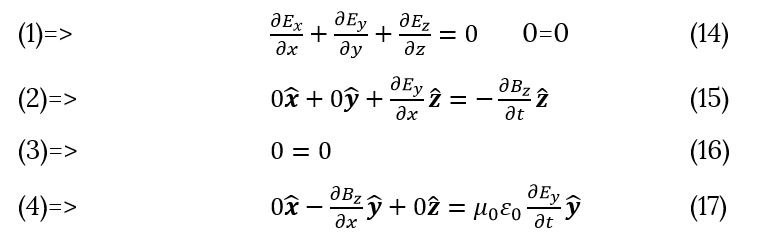
Equation (14-17) hold for any orthogonal functions, which satisfied to (10-13). Now we are ready to test some other functions.
Square wave
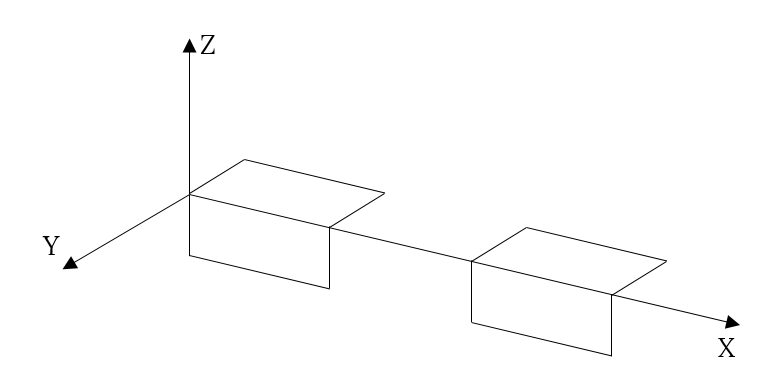
Square wave could be expressed as constant, which is not depending on x-coordinate or time. The value of such constant changed with some periodicity.
It does not matter are electric and magnetic fields in phase or out of phase, the result will be the same. All derivatives from the constants are zero, all equations degenerate to 0=0 and constants satisfied to Maxwell's equations.
It is quite interesting that constant value does not satisfied to mechanical wave equation, but completely satisfied to Maxwell's equation.
There are no need to represent square waves as infinite number of sine waves, square wave itself satisfy to Maxwell's equations. Dispersion of EM waves is the property of different waves speed at different frequency. Now we have one square wave which satisfy to Maxwell's equation directly and therefore only one speed. Why EM waves dispersed?
Triangular wave
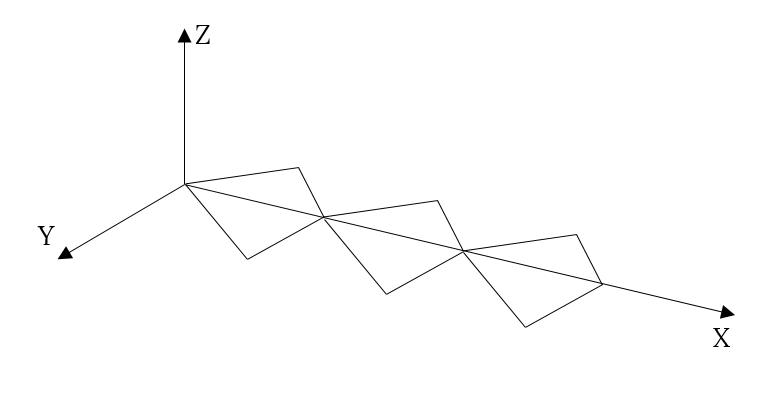
Triangular wave is simple linear dependency:
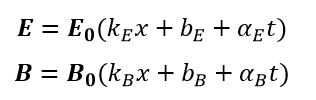
Where k, b and α are changing twice during wave period.
Equation (15) become:

Equation (17) become:
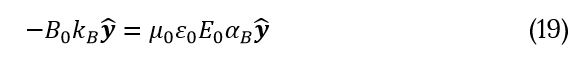
Both equations could be satisfied when:

It appeared that triangle wave also satisfied to Maxwell's equations at any circumstances. So why EM waves around us are not triangular?
Other functions
It could be easily demonstrated that any pair of orthogonal functions will satisfy Maxwell's equations if dependency on x-coordinate and time are as follow:
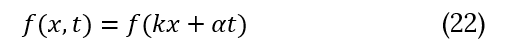
Exponential function also satisfied to Maxwell's equations, does not matter rising or decaying.
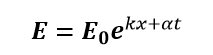
In other word Maxwell's equations does not provide us with the solution for EM wave in vacuum. Infinite number of various functions are the solution to Maxwell's equation.
Non-Orthogonal Functions
Non-orthogonal functions simply mean here that E vector is not perpendicular to B vector. The simplest function of that type is constant value.

In such case all equations degrade to 0=0 and constant magnetic and electric fields satisfied to Maxwell's equations. Please note that magnetic field not necessarily perpendicular to electric field in that case.
Let's consider triangular EM wave with electric and magnetic fields not perpendicular to each other. The direction of propagation will be x-axis. Both electric and magnetic fields do not have x-components.
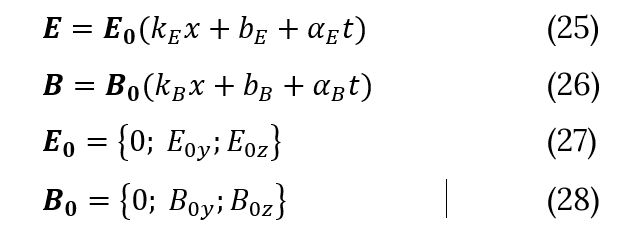
Then the E curl become:
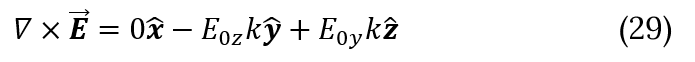
Similar equation could be written for magnetic curl and Maxwell's equation become:
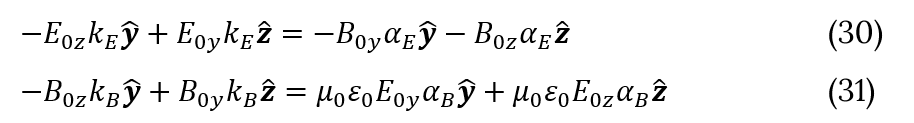
It is easy to see that above equations could be easily satisfied under any conditions. From here it follows that triangular waves with electric and magnetic fields not perpendicular to each other satisfied to Maxwell's equations. Please note that if E and B fields have only one non-zero coordinate, like in (10-11) then Maxwell's equations have only orthogonal solution.
Planar Waves
Take a second look at planar EM waves equations (8-11). Many textbooks have a drawing similar to Wikipedia, where E and orthogonal to it M components are traveling along x-coordinate like two sinusoids. Such picture does not provide us with the right impression. The equations for the plane wave does not depend on Y and Z coordinates and drawing should be something like this:
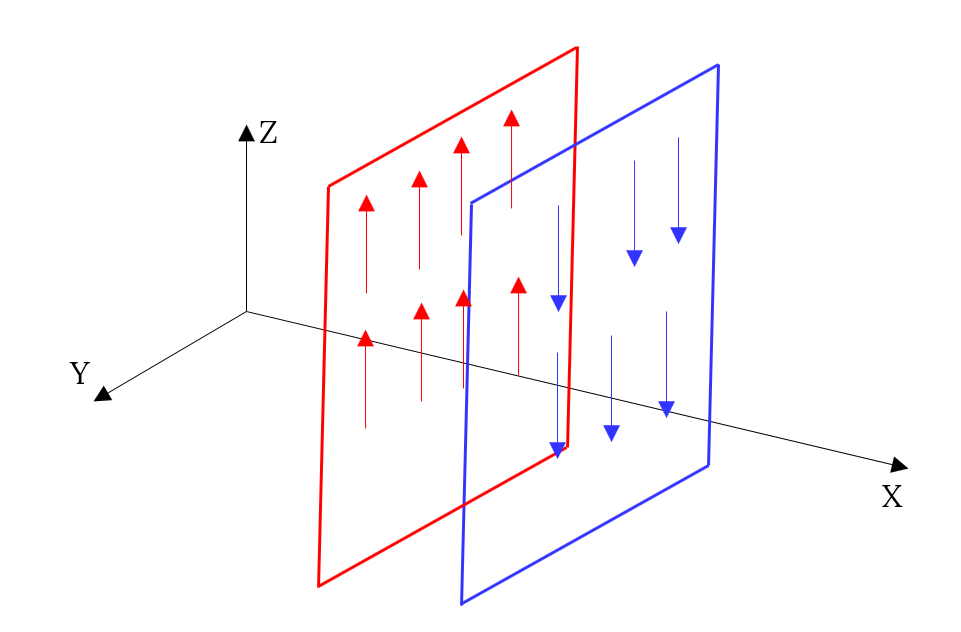
At each point of coordinate X we have infinite Y-Z plane with the same value of electric field. Electric and magnetic fields occupied all universe in the plane wave. How it is possible to talk about energy of infinite wave with non-zero amplitude? The energy also will be infinite. And this is not possible to change planar wave formula in order to introduce some directional component. EM waves in real world have a direction. As soon as one introduces directional part to EM wave formula, such wave will not be satisfied to Maxwell's equations because there is no symmetry between x-coordinate and time in such function.
What is moving?
Interesting question – what exactly is moving in EM wave? Electric field? Magnetic field? Both? Talking about magnetic field – is it any difference between constant magnetic field and constant magnetic field moving with some speed? Faraday’s law of induction telling us that such two cases could not be distinguish from each other. Then magnetic field could not move without changing its amplitude?
More questions than answers.
Conclusion
Maxwell's equations, the great mathematical tools for calculation of electric and magnetic fields do not work for EM waves in vacuum.