Some Digression
I am going to start a little bit earlier and take a brief look at one of the Zeno's paradox. This one is Achilles and the tortoise paradox.
In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.
Aristotle, Physics VI:9, 239b15
Resolution
Majority of paradoxes appeared when infinities were involved. In the case of Achilles's paradox, it was infinitesimal division of time and distance. Where there's infinities, there's paradoxes.
The resolution to the Zeno's paradox could be made in a very simple way – Achilles only able to move by steps, there are no movement possible of the length less than one step. Now it is obvious that Achilles will overrun the Tortoise in limited number of steps.
Such a process of introducing indivisible steps to the Achilles motion one could call “quantization” and this is exactly the way in which quantum mechanics was born – “quantization” as a counterweight to resolution.
Anyway, let's take a look at gases. The theory claims that temperature is equals to the average kinetic energy of the molecules with some scaling factor.
Black Body Catastrophe
Every physical body continuously emits electromagnetic radiation. The amount of emitted energy depend on the temperature and on the frequency of radiation.
Rayleigh-Jeans law is approximation to the radiation energy. There are two formulas; one is for frequency and the second one is for wavelength.
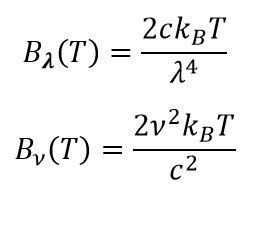
Rayleigh-Jeans law agrees with experiments at frequencies less than 105 GHz but disagree at higher frequencies. The frequency of such disagreement approximately corresponds to the frequency of ultraviolet light. As you can see from the formulas, radiated energy raise to infinity at high frequencies (low wavelength).
The situation called ultraviolet catastrophe for some reason. If the formula describing some physical process is wrong then from common sense the theory is wrong. In the science of physics, we have the opposite situation. If the fact does not fit the theory – too bad for the fact. The scientists were looking how to improve the formula, not the theory.
Solution
Max Planck derived correct form for the radiation distribution. I am not sure what the word “correct” stands for. Was new formulas agreed with experiments or just removed infinity?
Planck assumed that energy could be emitted only by discrete values called quanta. The quantum physics was born. Later Albert Einstein and Satyendra Nath Bose came with the postulate that hypothetical Planck's quanta were real particles called photons.
I would like to take a brief look at this very first brick in the foundation of quantum physics – Planck's law.
The Law
There are also frequency and wavelength formulas for spectral distribution of radiation:
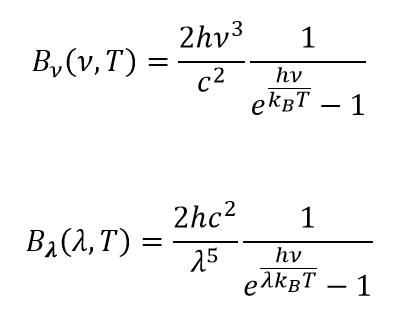
where kB is Boltzmann constant, h is Planck constant, and c is the speed of light.
Below is the graphic of radiation distribution vs. frequency at the temperature of 1000K.
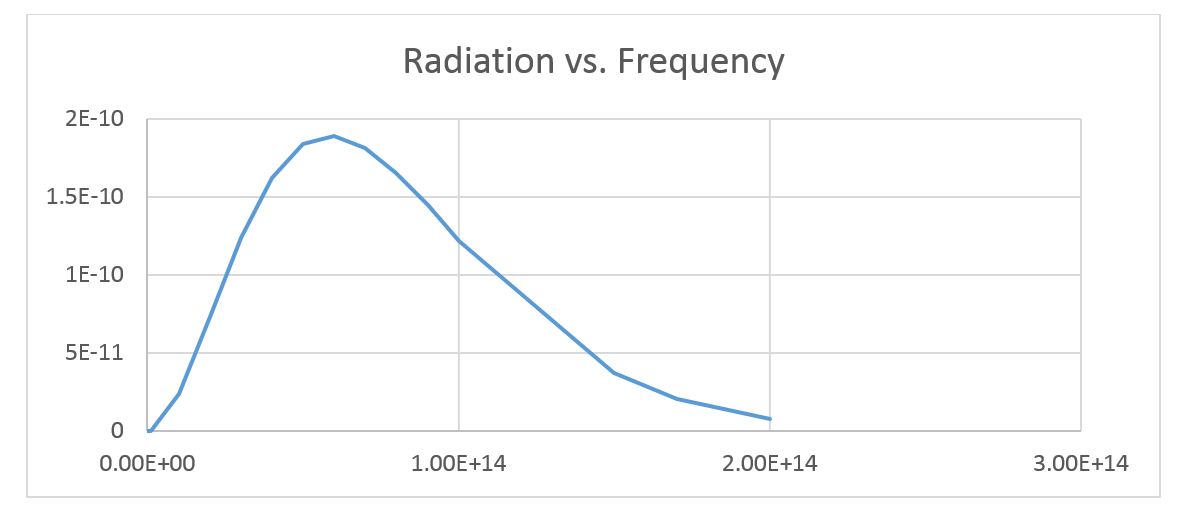
The maximum of the emission will be at frequency of 6∙1013 Hz.
The next graphic shows radiation vs. wavelength:
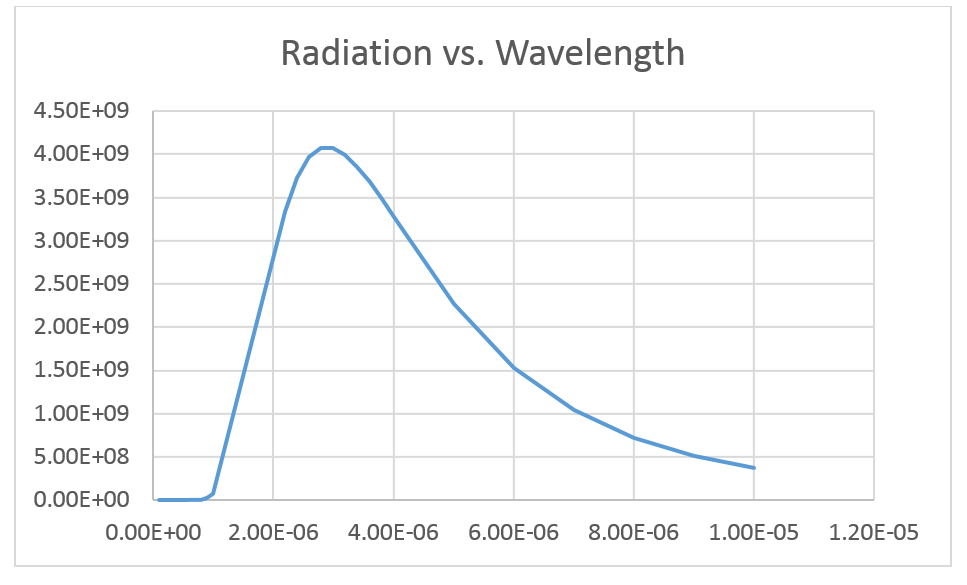
The maximum of the emission occur at wavelength 3∙10-6 m. We know the relation between frequency and wavelength:
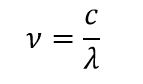
The frequency, corresponding to the maximum of the second graph will be 1∙1014 Hz. We have two results, which are different by the factor of 1.6 at the temperature of 1000K. A little bit too much for the theory. It appeared that this very first brick in the foundation of quantum mechanics was the cracked one.
I am just curious, which one of the above two equations tested experimentally, if any. Anyway, the quantum physics painfully came into being.