Introduction
Despite of the fact that Newton's second law of motion was introduced to the world of physics in 1687, it remains the most used law. Any computer simulation of motion uses second law and it does not matter how big or small the motions are – from micro scale mechanics to planet motion.
Second law has bother me for years. You probably familiar with that feeling when you feel something is not right. In this article I just put my feelings on paper.
Second Law
Strange thing – in the older textbooks on physics Newton’s second law was formulated as follow: the force equals mass times acceleration.
$$\Large F = ma \tag{1}$$Newer textbooks including Wikipedia use different notation:
$$\Large F = {{dP} \over {dt}} \tag{2}$$Which one is correct? We should take a look at Newton's “The Mathematical Principles of Natural Philosophy”:
DEFINITION II.
The quantity of motion is the measure of the same, arising from the velocity and quantity of matter conjunctly.
LAW II.
The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.
Indeed Newton mentioned momentum over time as the measure of the force.
Momentum Change
Formulas (1) and (2) looks very similar at first look. And they are indeed the same when mass of the body is constant. For the body which mass could vary the two formulas are completely different. Moreover, using time derivative of momentum lead us to paradoxical situation:

Imagine asteroid. Two identical cannons shooting cannonballs in the opposite direction at exactly same moment of time. How it will affect the motion of asteroid?
From common sense those two cannonball will not alter the motion of asteroid since the total momentum of cannonballs equals to zero. But take a look at formula (2). The mass of asteroid just has been changed by subtracting the mass of two cannonballs. Along with the changing of mass, the momentum of asteroid was changed. Where is the force?
Does Order Matter?
Let me step aside from the second law just for a moment and discuss more common problem. Are those two formulas identical?
$$\Large F = {{dP} \over {dt}} \tag{2}$$and
$$\Large {{dP} \over {dt}} = F \tag{3}$$In my opinion formula (3) states that applied force leads to the change of momentum, while formula (2) states that the force is the result of momentum change. Do you feel the difference?
While applied force produces the change in momentum, will change of momentum produces force?
Probably the order of variables does matter in some other physical formulas?
Variable Mass
As was shown before, Newton's second law is not handling variable mass correctly. But there is more.
Take a look how modern physics treated the system with variable mass. Good example could be found on Wikipedia. Momentum of the rocket was written as:
$$\Large d\vec{\bf{P}} = (m+dm)(\vec{\bf{v}}+d\vec{\bf{v}}) = m\vec{\bf{v}}+md\vec{\bf{v}}+\vec{\bf{v}}dm+dmd\vec{\bf{v}} \tag{4}$$where \( \large dmd\vec{\bf{v}} \) is much less compare to other members and could be omitted.
It follows that:
$$\Large \frac{d\vec{\bf{P}}}{dt} = m\frac{d\vec{\bf{v}}}{dt} + \vec{\bf{v}}\frac{dm}{dt} \tag{5}$$Any textbook on the subject uses this formula (5) without any doubt. And beside it is very simple math everybody already know:
$$\Large (ab)' = a'b + ab' \tag{6}$$Again, using mathematics without thinking. Let me bring some example.
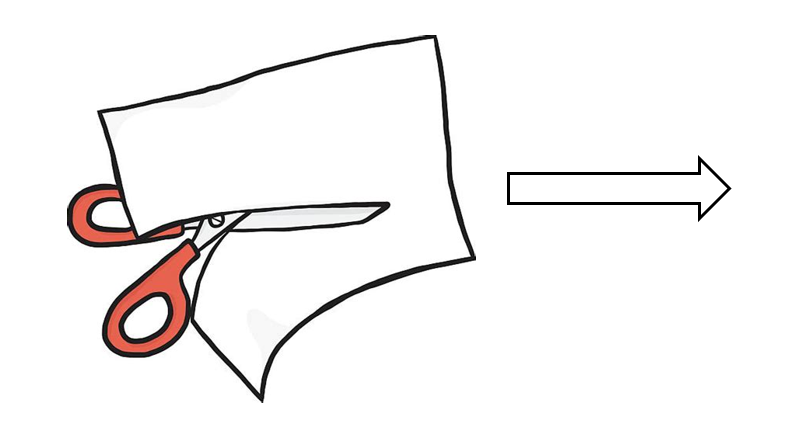
A piece of paper is travelling through space. We are cutting a small piece with scissors. The question is what will be the change in momentum? We can try to use previous formula (5). But...
What is \( \large \frac{dm}{dt} \) equals to? Does its value depend on the fact how fast we are cutting? Why change in mass acts in the direction of velocity which depends on reference frame?
In the above example it is clear from common sense that no force was appeared just from cutting small piece of paper. Then we could rewrite (5):
$$\Large F = 0 = m\frac{d\vec{\bf{v}}}{dt} + \vec{\bf{v}}\frac{dm}{dt} \tag{7}$$It follows from here that velocity could be changed even without any force which contradicts to the first law. Nothing makes any sense at all.
Conclusion
Something is wrong in Newton's second law when mass of the body could vary.
It looks like second law of Newton could not be applied to the body with variable mass.
While momentum of the body could be changed by providing the force, the change in momentum does not lead to appearance of the force.
Well known formula for time derivative of momentum in case of variable mass is not true.