The science of theoretical physics is completely dominated by mathematics. No more common sense and logic. Such approach was introduced for the first time by Isaac Newton in Principia and widely used in the science of physics since then. Due to omission in reasoning, the whole science became science fiction with seven dimensions and black holes, which emit something one day and nothing the other.
Very simple example of using mathematics without solid ground is the finding of the size of a square, which has the area of one square meter. The answer would be one meter, but mathematics provides us with the second solution of minus one square meter and this is the possible source of seventh dimension.
I am going to demonstrate the danger of using pure mathematics on the example of Noether theorem – sterile mathematical construct, not connected to any physics at all.
In simple words, Noether theorem states that every symmetry has a corresponding conservation law. Thus, the rotational symmetry leads to the conservation of angular momentum and so on.
Mathematician Emmy Noether proved the theorem in 1915. Someone could look on the subject at Wikipedia. The theorem is considered to be the most beautiful theorem in physics. There are few quotes from the web:
• She resolved a nagging puzzle in Albert Einstein’s newfound theory of gravity, the general theory of relativity. And in the process, she proved a revolutionary mathematical theorem that changed the way physicists study the universe.
• Many of the furthest-reaching stretches of cosmology and theoretical physics today, from speculation about string theory to the hunt for dark matter, depend in some way on Noether’s theorem.
• Deep insights are offered by the theorem and related ideas in ’understanding’ the observed structure of the theories, in this case the Standard Model of particle physics!
Noether was a great mathematician and her contribution to the science is undeniable, but using of pure mathematics without any logic or underlying physics could lead one to the fairy tales reality, as you will see.
In order to demonstrate how this theorem works in the world of real physics we will use particular example of symmetry in time. Such a symmetry will lead to the conservation of energy according to the theorem.
Once we dealing with mathematics we should read very carefully “terms and conditions”. There are many fine prints and strings attached.
The first question should be – what is a symmetry and symmetry in time in particular? When I hear the word “symmetry”, my imagination draws me a beautiful pictures of crystals, flowers and butterflies. Maybe at least mirror reflections and negative time, since we are talking about time symmetry.
However, according to mathematics, the symmetry in time means that something does not changing with time, the constancy, the invariability. The reality hurts and the number of π=3.14… is perfectly symmetrical in time because it is a constant.
To understand the theorem better, one should ask – what exactly is symmetrical? Do not even try to guess, the symmetrical thing is not from our world, it is a Lagrangian, another mathematical abstraction. So, symmetry “in time” does not mean that the time is symmetrical, the Lagrangian is.
What is the physical meaning of Lagrangian? There are no answers in the physics textbooks, they are telling us that Langrangian is the quantity that characterizes the state of a physical system. Very informative, it is like color or position, right? Sometimes Lagrangian defined as a function that satisfies the principle of least action, known as Hamilton's principle. Also not a lot of real physics.
Now we are going to do some physics, not path integrals.
Let assume that some physical body has kinetic energy K1 and potential energy P1. The Lagrangian of such system defined as:

Let kinetic energy to be increased by some value (ΔE). Assuming that energy is conserved, the potential energy reduced by exactly same amount:
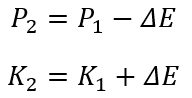
Since the Lagrangian of the system is “symmetrical” in time:

Now, looking at the results above, we have an understanding of the physical meaning of the Langangian's “symmetry in time”. Such a “symmetry” simply means that the kinetic energy of the system could not be transformed into potential and vice versa. Using our new knowledge, we can rephrase Noether theorem in the case of “symmetry in time”.
– If potential energy of the system is constant and kinetic energy of the system is constant then the sum of those energies is also a constant.
This is “indeed” very useful theorem for particle physics and dark matter study.
Particular case of Noether theorem for energy conservation and “symmetry in time” is the perfect example of what could happen if someone ignoring or losing the physical meaning of the subject under consideration.