Introduction
The numerous paradoxes associated with relativity physics. One of such paradoxes is relativistic length contraction. All relativity paradoxes could be resolved in a simple way – they are not real. Thus, length contraction and time dilation appeared only for distant observer. That is, how the things are visible from outside.
Nobody complaining that the sequence of events or causality was broken when one playing tape in reverse. So why observer could not see the things in the travelling ship in reverse?
Length Contraction
What is length contraction? We could just open relativity textbook or just Wikipedia as a mouthpiece of mainstream science.
“Length contraction is the phenomenon that a moving object's length is measured to be shorter than its proper length, which is the length as measured in the object's own rest frame.”
Einstein's Thought Experiment
Let's look how length contraction was measured by Einstein's thought experiment in his paper “On the Electrodynamics of Moving Bodies”.
We have the moving rod, traveling along \(x\) axis with the velocity of \(v\). The beam of light was emitted from one end of this rod, reflected at the other end, and received back. From the prospective of stationary observer, the length of the rod will be shorter by factor of gamma or Lorentz factor:
$$\large \gamma = \left( \sqrt{1-{{v^2}\over{c^2}}}\right)^{-1} \tag{1}$$and:
$$\large L = \gamma L_0 \tag{2}$$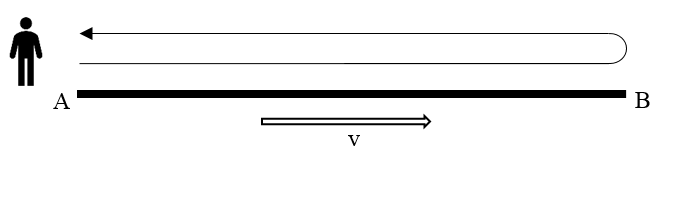
Fig.1 Moving rod light reflection
Armed and Dangerous
We have our secret weapon to demonstrate the absurdity of length contraction. And the weapon is Lorentz transformation! Lorentz transformation translates the coordinates in the moving system \((x^\prime,y^\prime,z^\prime,t^\prime)\) to the coordinates of stationary observer \((x,y,z,t)\).
Relativity physics use Lorentz transformation to deduce length contraction in a very specific way, they assume that measurement times for both ends of the rod are equal. As a matter of fact, the condition when those times are equal could not be met for material body of non-zero length. Below you will find the length contraction derived from Einstein’s thought experiment using Lorentz transformation without any boundary condition.
Lorentz Transformation
Lorentz transformation set the relation between moving and stationary reference frames:
$$\large t = \gamma \left(t^\prime + {{vx^\prime} \over {c^2}}\right) \tag{3}$$ $$\large x = \gamma (x^\prime + vt^\prime) \tag{4}$$ $$\large y = y^\prime, z = z^\prime \tag{5}$$Moving Rod
We need just two basic events for moving rod experiment:
• Light was emitted at the A-end of the rod at the coordinate \(x_A^\prime\) and time \(t_A^\prime\)
• Light received at the B-end of the rod at coordinate \(x_B^\prime\) and time \(t_B^\prime\)
In the stationary system we will see emission of light at the moment of \(t_A\) and coordinate \(x_A\).
The moment of the light reception in the stationary system will be at moment of \(t_B\) and coordinate \(x_B\).
According to Lorentz transformation (4):
$$\large x_A = \gamma (x_A^\prime + vt_A^\prime) \tag{6}$$ $$\large x_B = \gamma (x_B^\prime + vt_B^\prime) \tag{7}$$The length of the moving rod in stationary reference frame will be:
$$\large L = x_B - x_A = \gamma (x_B^\prime - x_A^\prime + vt_B^\prime - vt_A^\prime) \tag{8}$$ $$\large L = \gamma (L^\prime + v(t_B^\prime - t_A^\prime)) \tag{9}$$The constancy of the speed of light gives us:
$$\large t_B^\prime - t_A^\prime = {{L^\prime} \over {c}} \tag{10}$$Substitution to (9) yields:
$$\large L = \gamma L^\prime \left( 1 + {v \over c} \right) \tag{11}$$As you could see, the result is dramatically different from well-established formula in relativity physics.
As soon as the physical object is treated as finite length object instead of dimensionless point, Lorentz transformation always fails.
Reflections
All thought experiments in special relativity which play with light always have two beams of light, one of which was reflected. They always consider two-way propagation of the light beam.
Such reflections could be a real game changer in our observation. Let’s consider the following experiment of moving rod measurement:
• Stationary observer sends two beams of light in the direction of moving rod
• Beam #1 is reflected from nearest end of the rod (A) and received back by observer
• Beam #2 is reflected from farthest end of the rod (B) and received back by observer
• While beam #2 is traveling from A-end of the rod to B-end of the rod, the position of B-end of the rod will be changed due to rod motion
• As a result, the moving rod will look longer for stationary observer who uses such exotic way of measurement

Fig.2 Observation of the moving rod
It is not a real enlargement, just visual effect.
Are we observing the universe around us in the described way? Absolutely not! We are not using flashlight for the distant star observation. We are neither emitting any light nor waiting for its reflection. We are using the light from the star itself.
Try to imagine the previous experiment in the different way:
• Both ends of the moving rod emit light at the same time
• Observer received both beams and did calculation
What kind of length contraction will we measure this way? That’s right – zero.

Fig.3 Zero length contraction from light-emitting rod
Removing reflection from experiment makes the life of relativity physics harder.
Lorentz Number Three
So far we have two solutions for Lorentz length contraction. One is relativity formula (2) obtained by timing restrictions applied to Lorentz transformation. Second formula (11) was derived using Lorentz transformation without any boundary conditions.
It looks like by applying different boundary conditions different results could be obtained. Now I am going try to apply coordinate boundary condition. Who want a bet?
Let install “rod sensor” at zero x coordinate of the stationary system. When the end of the rod crossing our detector, time was measured. Knowing two time stamps and the velocity of the rod, it is easy to calculate the length of the rod in stationary system.

Fig.4 Measuring \(t_{START}\)

Fig.5 Measuring \(t_{END}\)
Due to relativistic clock synchronization, zero spatial coordinate and zero time are zeroes in both (moving and stationary) reference frame.
$$\large T_{START} = 0 \tag{12}$$Since our rod is moving to the right, let the second end of the rod be located in coordinate \(x = -L^\prime\) in moving frame.
Using Lorentz transformation for spatial coordinate (4) yields:
$$\large 0 = \gamma (-L^\prime + vt_{END}) \tag{13}$$and:
$$\large t_{END} = {L^\prime \over v} \tag{14}$$Substituting our finding to Lorentz transformation for time (3) gives us:
$$\large t_{END} = \gamma \left( t_{END}^\prime + {{vL^\prime} \over {c^2}} \right) = \gamma \left( {{L^\prime} \over {v}} + {{vL^\prime} \over {c^2}}\right)\tag{15}$$We know the speed of the moving reference frame and the length of the rod in stationary system will be:
$$\large L = v(t_{END} - t_{START}) = vt_{END} \tag{16}$$and:
$$\large L = \gamma L^\prime \left( 1 + {{v^2} \over {c^2}}\right) \tag{17}$$Anybody surprised? Different boundary conditions i.e. different experiment setup indeed produce different results of Lorentz length contraction.
Conclusion
The calculated value of the length contraction depends on the method of the length measurement during thought experiment and thus non-physical.