Introduction.
One of the weirdest concept of relativity is the “curved” spacetime. There are numerous fallacies in such “curving”. The most obvious one is that vacuum is nothing more but empty space or just nothing. How nothing could be bend? Einstein's general theory of relativity explains gravity as a distortion of space. Please take a closer look: mass distort spacetime and distorted spacetime pulls masses together. Getting rid of the middle term: “Masses cause masses to pull”. A little bit circular – isn't it?
Trampoline Analogy.
Everyone familiar with trampoline or rubber sheet analogy when two heavy balls create a warp in such sheet and pull to each other. However, those two balls could only bend trampoline when “external” gravity exist.
Extra Dimensions?
There is an opinion that to warp something required extra dimension of being warped into. Unfortunately, I was not able to find exact mathematical definition of “bending” and how such bending related to the dimensions.
Relativity textbooks telling us that curved space do not require extra dimension. All we need is just Pythagoras theorem.
The distance between two points in three-dimensional space could be determined as:
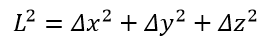
If theorem holds then our space is not curved. If it does not holds then we have a curvature.
It is impossible for the human been to imagine how our ordinary three-dimensional world could be curved and I am going to use one-dimensional example. The position of the point on the line is just x coordinate of that point and the distance between two points become:

Now let us bend our line into second dimension or y coordinate:

What happened to the distance AB? The distance remains unchanged of course. We are living in one-dimensional world, remember? All we can do is to measure the distance along the curved line, the upper dimensions are closed to us. Indeed, the coordinate of A is still xA and the coordinate of B is still xB, nothing changed in our world, we just don't know if the world is bended, but willing to find out. It does not matter if line curved or not – the coordinates along the line remains the same. In my example, there is no compression or abridgement of the line. Compression would not change anything by the way, the ruler will also be compressed.
It is clearly visible that using Pythagoras theorem as a definition of being curved is nonsense. The using of Pythagoras theorem in “curved” mathematics close related to the theorem that “straight line is the shortest distance between two points”.
Looking at the above picture, we could see that L1 is still a straight line in one-dimensional world or world “along the line”. L2 simply does not exist in this world. L2 become straight line only when stepping above into two-dimensional world. Only there L1 is curved and L2 is straight.
Finally, “being curved” indeed requires extra dimension. The criteria of the curved space become:

The distance between two points not equals to the distance between same points measured in the space with extra dimension. Pythagoras theorem could still be used for distance measuring, but with additional dimension on the right side of equation.
Practicing in Measurement.
Now imagine the student who read textbook article about curved space and trying to measure if the world curved. According to textbooks, some area of the space curved if:
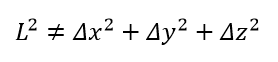
Next step would be find some “curved” area in space.

My coordinate system will be Cartesian. The coordinate system is just imaginary construction and it could not be “curved” along with the world. The student want to measure the distance OA from the coordinate’s origin to the point A. The first step of the measuring would be to measure coordinates X and Y of the point A, or the distances XA and YA. All points of interest are located at coordinate z=0 and the problem become two-dimensional.
Voila, the measurement done! It should be noted that XA and YA distances are “non-curved” distances; we just do not touching curved part of the space during measurement. Calculating OA distance for the case of non-curved space:
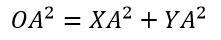
After calculation, the actual measurement should follow in order to compare results:
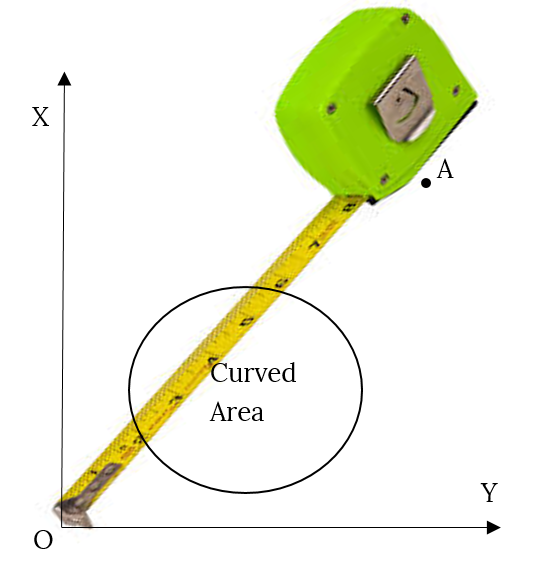
If space is indeed “curved” then we should see that distance OA is longer compare to our theoretical prediction. However, distance OA is the distance in our imaginary Cartesian coordinate system and could not change. Definitely, something happened to the measuring tape!
Curved space logical fallacy raised even more questions. How curved space affect the length of the measuring tape, the length of real objects?
Imagine that curved space area is circling around the origin, as Earth orbiting the Sun. Observer will see that the length OA measured by the tape changing the value periodically. Does oscillation of the tape's length means that there are forces acting on the tape?
Conclusion.
The curved space is illogical and does not exist in nature. The definition of “being curved” using Pythagoras theorem is wrong and should be redefined using extra dimension.