Introduction
The entropy, I guess, could be a Guinness record holder by the number of discussions in 300 years. There are tremendous number of articles about the discovery, history and development of the concept of entropy. I am not going to dig the history or certain articles about the subject, instead I am going to demonstrate the flaws in the concept.
Thermodynamic Definition
The entropy was introduced as some link between the amount of heat supplied to the body and the temperature of such body. Entropy was defined as:
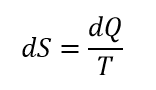
where S is entropy, Q is heat and T is temperature.
Entropy was never defined as absolute value, only in terms of differential.
The flaw is sitting in the temperature term. The kinetic theory of gases telling us that the temperature equals to average kinetic energy, just with some dimensional coefficient. But the temperature itself depend on the heat we added to this body. Prior to heat addition the body had some smaller temperature compare to the end of such addition. Which temperature should be used in the above formula? This question not even raised anywhere in the literature starting with Clausius.
Meanwhile the answer to this question defines the second law of thermodynamic.
The Second Law
The second law of thermodynamic states that entropy is never decrease. Let's consider the following experiment: we are adding infinitesimal amount of heat to some thermally isolated body, let's say using Peltier element, then withdrawing exactly same amount of heat and so on. The process is cyclic.
Let us make a guess that temperature in entropy definition is the temperature before heat was added. Then during heating, we added entropy:

Working body will increase its temperature after heat was added. During cooling stage of the process, the entropy will be decreased by:
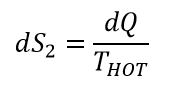
Since THOT > TCOLD , dS1 > dS2. The entropy of our working body will increase indefinitely. We just formulated second law of thermodynamic – the entropy constantly increasing! Increasing to infinity!
Look at our working body. Some amount of heat was added in the first half of the cycle. Absolutely same amount of heat was withdrawn in the second half. That are the changes inside this working gas? The energy remains the same along with the temperature. We keep the same volume and having same pressure. It is the same gas!
The gas at the beginning of the process could not be distinguished from later at the end of the process. However, some mystical property called entropy is different. The entropy is not measurable quantity and the only way to know the entropy is calculations. If every parameters of our gas are the same, then what is different? And there is more. Absolutely the same gas with identical properties not suitable anymore for doing mechanical work since its entropy increased.
If the temperature in the entropy formula was temperature after heat addition, then the result of the same process will be decreasing of entropy. So it is quite easy to build another quantity which will be constantly decreasing.
Standard Textbook Definition
The entropy often defined as: “the measure of a system’s thermal energy per unit temperature that is unavailable for doing useful work”.
The idea behind definition is clear – the thermal energy dispersed and not all of it is available for doing mechanical work.
But such definition flawed from very beginning. Starting with the words “per unit temperature”. What exactly does it mean? We are not interested in the energy per temperature unit, we are interested in the whole energy which is unavailable for doing work. If we know some value per unit temperature – should we multiply result by the temperature? Of course, we can't! Moreover, “per unit temperature” could only be referred to entropy differential! In order to find the total entropy we should integral from this differential. And “per unit temperature” should be changed to “multiplied by temperature logarithm” since integral from reciprocal equals to logarithm.
We are adding to some gas small amount of heat – dQ. The definition telling us that part of such addition is not available of doing mechanical work. That is at room temperature:

Should we pay attention to the phrase “per unit temperature”? Is the whole amount of unavailable energy equals to dQ? Does the whole energy became unavailable?
Here is different approach: if the amount of dQ/300 is unavailable, then 299dQ/300 is available by simple math. The efficiency of thermal engine should be 99% then.
The standard definition “entropy is the measure of a system's thermal energy per unit temperature that is unavailable for doing useful work” could also be rephrased keeping in mind that temperature equals to average energy of molecules.
“Entropy is the measure of a system’s thermal energy per system average energy that is unavailable for doing useful work”. How does it sound?
Ideal Gas
It worst to mention that the concept of entropy was introduced for ideal gas. The “ideal” does not mean that the molecules are perfectly round and the collisions between them are perfectly elastic. Ideal also means that there is nothing more except the collision. No forces, no fields, no gravity – just collisions. The entropy was not defined under the influence of the forces. Imagine metal spheres in jar. Shaking this jar under the influence of gravity will decrease entropy, since the balls will became more ordered. The positions of the balls will now be dictated by the minimum of potential energy instead the minimum of entropy. Where is the second law in this case?
Carnot Cycle Definition
The concept of entropy was introduced by Rudolf Clausius and was inspired by his study of Carnot cycle. Even in modern textbooks entropy often defined through Carnot cycle. Carnot cycle could be found here.
There are two important steps in the cycle of Carnot:
• Step 1 – the heat transferred from high temperature reservoir to working gas at constant temperature
• Step 3 – the heat transferred from working gas to low temperature reservoir at constant temperature
The second law of thermodynamic often formulated in the following way – “heat always flows from the hotter body to the colder one”. There also Newton's law of cooling which states that the flow of heat is proportional to the temperature difference. According to this claim – what heat flow will be equal to when temperatures are equal? The heat flow will be also zero! Carnot cycle is the cycle with zero energy flow. The efficiency of such cycle will be zero over zero and it could be any value you want.
Carnot cycle was always compared in the literature to real engines like steam engine or diesel engine. This is really weird because real engines are not cyclic! Each new engine cycle starts with new portion of working gas while old portion of the gas was wasted to the atmosphere.
The meaning?
As was mentioned before, there is no physical meaning for entropy. Indeed, let's try just pure math. We have a set of numbers in the range of 1 to 100. The total quantity of the numbers equals to 1000. Average value of this set of numbers equals to 50. I am adding the number 40 to that set. What is the meaning of 40/50? 40 here is dQ added and 50 is the average (temperature).
Why it is so important that artificially constructed mathematical expression always increased? Why the behavior of abstract variable is so important? The answer is – it is not. The importance of the entropy increasing was introduced later, when the term “entropy” was associated with the order of the system.
The Order
After association of the term “entropy” with the order of the system a lot of speculations appeared. Some of the speculations are:
• The universe tendency is chaos
• The evolution contradicts to thermodynamics
As you could see, the entropy definition as an order of the system depend on the definition of the term “order”. Prior to such definition the order should also be defined. In modern textbooks entropy is often formulated as “entropy is closely related to the number Ω of microscopic configurations”. And the Boltzmann's definition of entropy is:

where kB is Boltzmann constant and Ω is the number of possible microscopic configurations.
Here I am trying to understand what “microscopic configurations” could possibly be on the example of ideal gas. The entropy of ideal gas defined as:
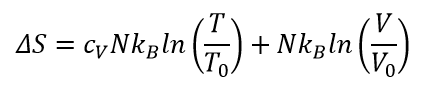
Keeping the volume constant making life easier and expression become:

Compare this equation to the Boltzmann's definition of entropy we could state that “the number of possible microscopic configurations” equals to some function of temperature!
But the temperature equals to average kinetic energy! I am totally confused. The number of microscopic configurations equals to the average kinetic energy? Only one number could be assigned to the average kinetic energy! Does this fact make the number of microstates equal to ONE?
Besides the number of microscopic configurations should be expressed only by microstate variables! As soon as it expressed by the average, it became macroscopic.
The Order and Second Law
The second law of thermodynamics is probably the champion by the number of publications. Does evolution contradict to the second law?
Second law contradict even to itself and this fact could be easily demonstrated. Imagine the system consisting of countable number of gas molecules, let's say 1000. There certainly will be countable number of so-called “microstates”. Some of such “microstates” having the maximum entropy value. How the entropy could increase above this numbers? But it should increase according to the second law.
In other words – if maximum disorder was achieved, how entropy could increase any further?
More on Order
We were just talking that the term “order” should be explicitly defined before one dealing with entropy as an order. Consider salt(s) and pepper(p) in a jar in 1:1 proportion. At the beginning salt is on the left, pepper on the right. Then we shake jar for a long time until we got a combination s-p-s-p-s-p-… Is it order or disorder? Is it more ordered compare to initial situation?
Shannon’s Entropy
Here is a very good article about multiple definitions of entropy in science. The most unphysical one is informational entropy or Shannon entropy. The formula of Shannon entropy looks identical to the Boltzmann one.
Here the Shannon's words:
- My greatest concern was what to call it. I thought of calling it “information”, but the word was overly used, so I decided to call it “uncertainty”. When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, - “You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name. In the second place, and more importantly, no one knows what entropy really is, so in a debate you will always have the advantage!”
The key difference between thermodynamics' and informational entropy is in fact the understanding of the word “order”. While Boltzmann entropy rely on microstates (whatever that means) which most likely related to the velocity distribution, Shannon entropy is just the position of certain information in the string.
The discussion how informational entropy related to the thermodynamics one has no solid basis. All formulas how much energy required to store one bit of information are pure speculation.
To finish with Shannon entropy, it should be mentioned here that informational entropy concept is widely used in machine learning algorithms. More precisely, some algorithms of machine learning are entropy minimization algorithms. Looking back at the second law and keeping in mind that entropy of something decreased – should the entropy of my computer running learning algorithm increased even more over time? (because the total entropy should not decrease) If you are doing some machine learning on your computer and you trained one hundred neural networks, imagine how high the entropy of your computer is! It is also interesting – there are some software for rolling back your computer to its previous state. Does such software restore the entropy of my high-entropic computer?
Entropic Forces
Entropic forces are very popular concept in modern physics. Physicists are trying to explain different phenomenon’s using the concept of entropy. The idea is simple – if entropy of some system tends to increase, then (of course) the force appeared in the direction of entropy increasing.
The absurdity of such claim could be easily demonstrated. My system consists of black and white balls in a jar. One third are black and two third are white. We are taking three balls at a time from the jar. By doing such experiment we will notice soon, that most of the combinations will be black-white-white. Definitely, there is a force between white balls and my hand, it's just not strong enough to pull them all the time.
In simple words: if some situation is more probable than the others – you don’t need any force for explaining that.
Conclusion
Summing all the above, the concept of entropy has no solid ground.