Introduction
There are tons of papers on the second law of thermodynamics. Here I am trying to understand is entropy some essential property of any material and body or just some mathematical construction that was built as attempt to explain the nature of things. I am not going to touch any order or disorder associated with entropy and all "entropy" further in this text is referred to good old entropy for an ideal gas.
It is very clear where the idea of entropy came from. Not all thermal energy of a gas could be transformed to mechanical work, at least we just don't know the way yet.
Thermal energy of hot body could not be transformed into mechanical work. The work just does not came out of the hot, the cold body is always required. Obtained mechanical work equalized hot and cold temperatures, making further work nearly impossible.
The Second Law
I was always wondering why the entropy of the universe increased. Second law does not state that. Second law saying that entropy is never decreased, and it make perfect sense. When we are running simulation on the molecule’s collision in ideal gas, we could start it with the same velocities for each single molecule. After some time, the velocities are mixed, and soon we will get Boltzmann’s distribution of velocities, which does not change with time no more. Something in the system changing to some extent during mixing and stops when the mixing is done. Entropy should behave similar to exponential function, but it should never increase to infinity.
Another question without answer is – how some theory and formulas derived for ideal gases could also applied to solid bodies? There are a lot of solid bodies in the universe and its entropy is increasing. Ludwig Boltzmann derived his formulas based on the ideal gas equation and gas molecules velocity distribution. Both are not correct for solid bodies.
Interestingly, the creation of planets from the dust cloud increased or decreased the order in the Solar system?
Entropy Definition
Entropy has no definition. The only formula one could find in literature describes the entropy differential, not the entropy itself:
$$\large dS = {dQ \over T} \tag{1}$$where \(dS\) is entropy increased when some amount of heat \(dQ\) was added to the system and \(T\) is the temperature of the system.
Even at a glance above formula looks a bit strange. The amount of heat is the energy while the temperature reflects an average energy of the system. The entropy is energy over energy and it is dimensionless if we omit the Boltzmann’s constant as a proportionality between energy and temperature.
On second look, you could see that the same amount of heat will less and less contributes to the entropy increase as temperature rises. This looks exactly like we expected, but…
The Temperature
The entropy could not be measured neither directly nor indirectly. It could only be calculated. The calculation of the quantity which defined in the differential form required integration and here I am going to do such integration.
Integration could be replaced with the summation when all deltas are infinitesimally small. The energy of an ideal monoatomic gas defined as:
$$\large E = {3 \over 2}{k_{B}T} \tag{2}$$where \(k_{B}\) is Boltzmann's constant.
The temperature versus heat will be straight line:
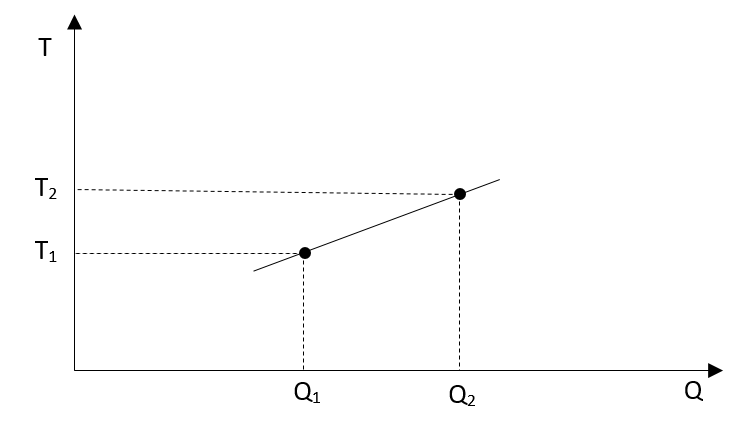
It does not matter how small we are going, there are always two values for temperature, T1 and T2, the temperature before we added some very small amount of heat and the temperature after such addition.
Which one of those temperatures should we use during integration? On the first look it probably does not matter because everything is so small… We shall see.
Entropy
We are going to make the following experiment – we have a gas in the jar with absolute thermal isolation. The stating temperature is T1. After addition of very small amount of heat the temperature will rise to T2. If we remove the same amount of heat, the temperature will drop back to exactly same value as it was before addition – T1 just because the dependency between energy of the gas and temperature is linear. We will keep going, adding and removing the heat and keep our eyes on entropy.
Entropy #1
Our first scenario of integration will be using the temperature value before addition or removal of heat.

The dotted line represents our integral.
1. Heat added=\(dQ\), temperature at start=\(T_1\), temperature at end=\(T_2\), entropy rise:
$$\large dS_1 = {dQ \over T_1} \tag{3}$$2. Heat removed=\(dQ\), temperature at start=\(T_2\), temperature at end=\(T_1\), entropy drop:
$$\large dS_2 = - {dQ \over T_2} \tag{4}$$3. Balance:
$$\large dS = dS_1 + dS_2 > 0 \tag{5}$$Number one entropy in our example will grow as the number of heating/cooling cycles grows. This entropy looks like the classical one.
Entropy #2
The second scenario will be using the temperature at the end of heat addition – adding heat, wait and then measure the temperature.
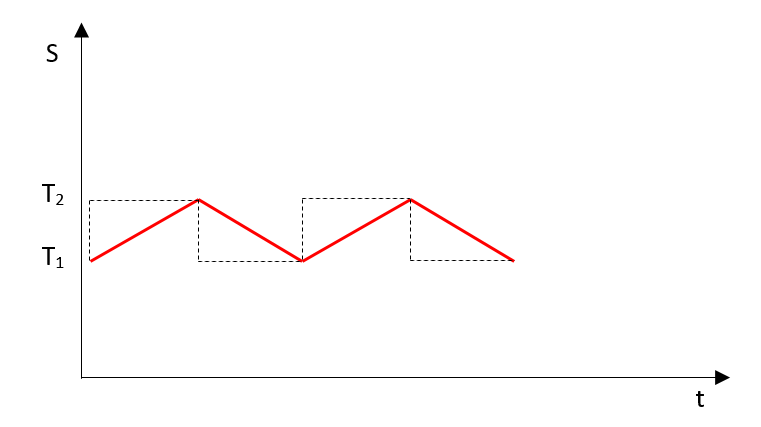
Again, the dotted line shows our summation. Looks very similar, just the order of summation was changed, wasn't it?
1. Heat added=\(dQ\), temperature at start=\(T_1\), temperature at end=\(T_2\), entropy rise:
$$\large dS_1 = {dQ \over T_2} \tag{6}$$2. Heat removed=\(dQ\), temperature at start=\(T_2\), temperature at end=\(T_1\), entropy drop:
$$\large dS_2 = - {dQ \over T_1} \tag{7}$$3. Balance:
$$\large dS = dS_1 + dS_2 < 0 \tag{8}$$Now entropy will diminish over time, what a surprise!
Entropy #3
Another possibility is to use median temperature in our calculations: \((T_1+T_2)/2\).
Conclusion
The uncertainty of the temperature value in the definition for entropy could lead to multiple entropies. In simple thought experiment the value of entropy will grow to positive of negative infinity as well as will stay unchanged, depending on calculation.
Looks like Regular integration as we know it, is not suitable instrument for entropy calculation.
The concept of ever-growing entropy is just mathematical construction, which could be easily altered to ever-diminishing or unchanged entropy.